pyqo Tutorial

pyqo is a python library similar to the quantum optics toolbox for Matlab. It lets the user define state vectors and operators and provides functionality to solve typical problems occurring in quantum optics, e.g. solving Schroedinger or master equations.

Importing pyqo

To be able to use pyqo from a python script the pyqo library has to be in your PYTHONPATH or in the same directory as the script that uses it. Then it can for example be imported as:

>>> import pyqo as qo

In all following examples it is assumed that pyqo was imported in that way.

Defining states

All objects in pyqo are defined as tensors of different ranks. Taking advantage of the power of numpy, they inherit from the mighty numpy.ndarray. Obviously their dimensionality is limited by the memory available on your system so it is impossible to calculate in infinite dimensional Hilbert spaces. For quantum states pyqo provides the class pyqo.StateVector. It can be used to directly create states from nested lists or tuples (or anything else that a numpy array can handle):

>>> psi = qo.StateVector([1,0])
>>> print(psi)
StateVector(2)
[ 1.+0.j  0.+0.j]

Alternatively there are some functions that create commonly used state vectors:

>>> psi = qo.basis(4,0)
>>> print(psi)
StateVector(4)
[ 1.+0.j  0.+0.j  0.+0.j  0.+0.j]
>>> psi = qo.coherent(10, 0.5)

Composing systems can be done with the tensor product between two states. For this the operator ^ can be used.

>>> psi1 = qo.basis(2,0)
>>> psi2 = qo.basis(2,1)
>>> print(psi1 ^ psi2)
StateVector(2 x 2)
[[ 0.+0.j  1.+0.j]
 [ 0.+0.j  0.+0.j]]

Note

The ^ operator follows the built-in operator precedence. That means “*” and “+” have higher precedence!

Defining operators

Operators are represented by the pyqo.Operator. Like in the case of state vectors operators can be constructed directly from a list or tuple:

>>> A = qo.Operator([[1,0], [0,-1]])
>>> print(A)
Operator
2 -> 2
[[ 1.+0.j  0.+0.j]
 [ 0.+0.j -1.+0.j]]

Operators have some constraint on their shape - it has to be of the form .

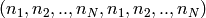Many commonly used operators are already defined:

>>> print(qo.sigmax)
Operator
2 -> 2
[[ 0.+0.j  1.+0.j]
 [ 1.+0.j  0.+0.j]]
>>> print(qo.create(3))
Operator
3 -> 3
[[ 0.00000000+0.j  0.00000000+0.j  0.00000000+0.j]
 [ 1.00000000+0.j  0.00000000+0.j  0.00000000+0.j]
 [ 0.00000000+0.j  1.41421356+0.j  0.00000000+0.j]]

Composing operators of different systems can be done in the following way:

>>> s_z = qo.sigmaz
>>> s_p = qo.sigmap
>>> print(s_z^s_p)
Operator
2 x 2 -> 2 x 2
[[[[ 0.+0.j  0.+0.j]
   [ 0.+0.j  0.+0.j]]

  [[ 1.+0.j  0.+0.j]
   [ 0.+0.j  0.+0.j]]]


 [[[ 0.+0.j  0.+0.j]
   [-0.+0.j -0.+0.j]]

  [[ 0.+0.j  0.+0.j]
   [-1.+0.j -0.+0.j]]]]